As we approach an age of automation, the target goal is giving our robots tasks such as “bring me coffee” without specifying the details of how to do it, and expecting our robots to do so. Assuming we own a couple of RoFI modules, the task of taking an object from point A and bringing it to point B is a basic but surprisingly complex task. The modules need to agree on how to do it, evade collisions, and not spill any coffee while bringing it, which leads to rather interesting algorithmic problems.
A natural way to approach this problem is for the RoFI modules to connect into an arm, grab the given object, and move it to the desired position.
Assume a couple of modules connected in a chain, on a fixed or independently moving base. We will call such a configuration an arm or manipulator, and its tip the end effector. Joint position will refer to the degree of rotation of a given joint, while end effector position will refer to its location and rotation in cartesian space. The discipline dealing with the relationship of module joints and end effector position is called kinematics.
Kinematics
We divide kinematics into two categories: Forward and Inverse Kinematics.
-
Forward kinematics is a straightforward problem of deducing the position of the arm in space from the joint positions. This problem always has a unique solution.
-
Inverse kinematics is the problem of finding the right joint positions when given a target position for the end effector: solving this is the first step of being able to grab an object. Inverse kinematics is a computationally difficult problem, as it generally has an infinite number of solutions. Since an analytical solution is impossible to find when the arm has a high number of joints, various numerical methods are used. These approaches are iterative, and can often be formulated as a minimalization problem with respect to the distance of the target.
Historically, methods based on the Jacobian matrix have been used. The Jacobian matrix consists of partial derivatives at each joint, and intuitively expresses how the end effector will move when slight changes in the joint positions are made. We can approximate the inverse of this matrix with various methods, and obtain a direction to move the joints in order to move the end effector closer to the target position. The method is heavily discussed in literature and works well for manipulators with a few joints, but does not scale well, since the involved matrix operations are quadratic or cubic with respect to the size of the matrix and need to be computed repeatedly.
More scalable solutions work in a greedy fashion and consist of geometric operations. The simplest of these solutions is Cyclic Coordinate Descent: the algorithm iterates through all the joints and moves them so that the distance to the end effector is locally minimized. However, this method has its own share of problems: the produced poses are unnatural, the number of iterations is unpredictable, and obstacles are difficult to deal with.
The state of the art solution is FABRIK: Forward and Backward Inverse Kinematics. The details of the algorithm can be found in the authors’ article: FABRIK: A fast, iterative solver for the Inverse Kinematics problem.
FABRIK is a greedy iterative algorithm. It consists of simple geometric computations in each iteration, and converges quickly. Its complexity scales linearly with respect to the amount of joints. Even with relatively limited computational strength, FABRIK can compute the desired joint rotations in microseconds, unnoticeable in the eyes of a human. This makes it perfect for our use case.
Why Inverse Kinematics is not enough
In a perfect world, computing the target positions for our arm would be enough to grab and move objects. Unfortunately, the real world consists of obstacles to avoid, limitations of hardware and forces of gravity. Even if we extend FABRIK with obstacle avoidance, we can compute collision free positions, but it remains unclear how to perform the motion itself: we cannot simply rotate the joints to the computed positions.
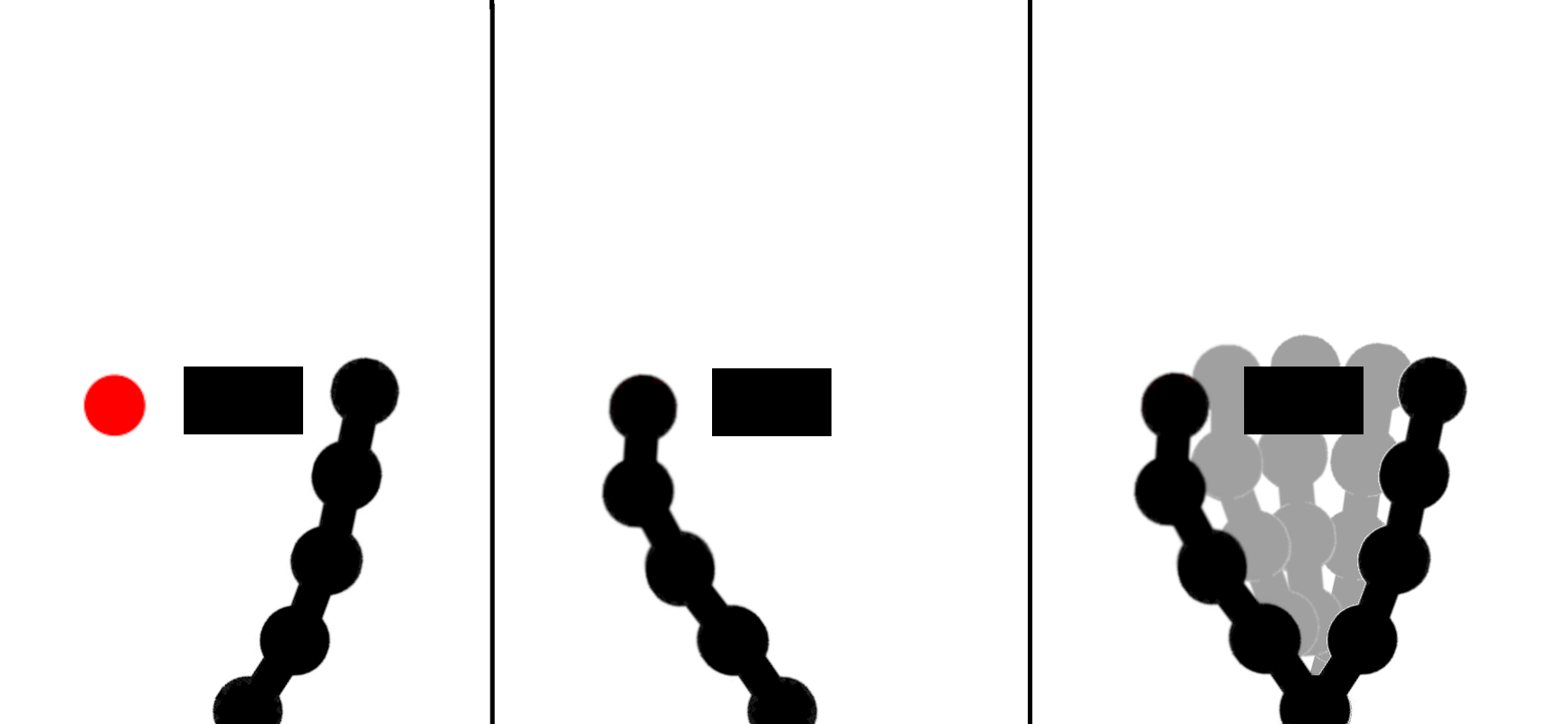
However, the ability to compute Inverse Kinematics will serve as a piece to the puzzle of how to control our arm.
Trajectory planning of robotic arms
The task of finding the final trajectory for the arm is still an open problem. With high quality Inverse Kinematics algorithms at our disposal, one of the common approaches is to compute the final position with IK, and reconstruct the path with a state-space search. This works well for industrial arms with a limited number of joints: we can find the target joint positions, use RRT or A* methods to produce a feasible path between the initial and target positions, and perform the movement.
However, the state space grows exponentially with the number of joints. When we consider the fact that each RoFI module has 3 joints, this approach gets hard to compute even for a few connected modules.
That’s why we reduce the task to two different problems:
-
path planning with respect to the end effector only
-
reconstructing the remaining joint positions at each step of the way
An intuitive approach to the first problem is to construct an occupancy grid: a graph where each point is assigned a cost based on nearby obstacles. In a controlled environment, we can place a high resolution camera in the room and get a complete map of the room externally. In an unknown environment, nearby obstacles can be detected by sensors in our module connectors, and the occupancy grid can be updated as the robot moves.
Once we’ve constructed the grid, we can use standard graph algorithms to find the shortest paths. With some tweaking, this method finds reasonable paths for the end effector:
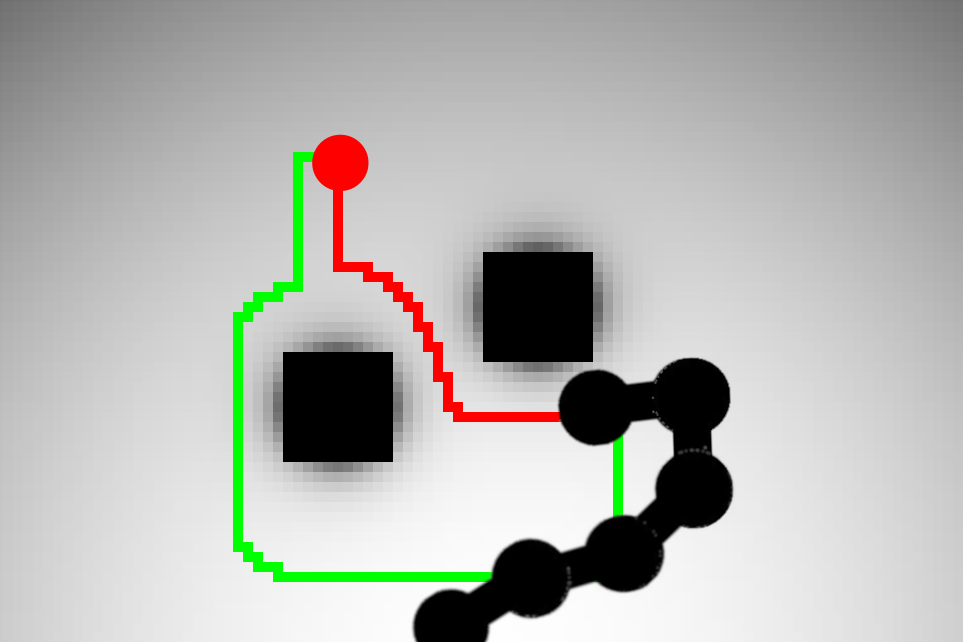
Once we’ve found a path for the end effector, we can smooth it out and reconstruct the remaining joint positions for each step of the way with IK. Historically, this approach has been frowned upon due to the high cost of some IK methods, but FABRIK can easily be computed hundreds of times to perform the needed incremental changes, while respecting nearby obstacles and joint limits. Some of the found paths might not be optimal or even viable, but due to the algorithm’s low cost, we can use the individual RoFI modules to try and reconstruct various paths in parallel.
