State spaces of RoFIBots
In the context of reconfiguration, there are different ways we can look at a configuration. Depending on the use case, it might be beneficial to not differentiate between two different configurations if they share some attribute, such as a shape. For RoFIBots, we introduce these three equivalence classes for configurations which have proven to be useful:
| Equivalence class (state) | State space transition (step) | Defined by |
|---|---|---|
| Configuration | Rotations and dis/connections | RofiWorld |
| Shape | Rotations and dis/connections | Shapes of configurations |
| Topology | Module reconnection | Topology graph |
Configuration class
This is the basic level: configurations are not in groups, and are considered equal only when they are exactly the same.
Shape class
The shape class is more interesting: when two configurations specify robots with the same shape (we can obtain one by rotating the other in space), they are in the same class. This means that we do not care about specific IDs of modules, components or sometimes even parameters of joints, as long as the resulting robot “looks the same”. This might be useful in situations which require the robot to have a certain shape, but it does not matter exactly which part is formed by which module.
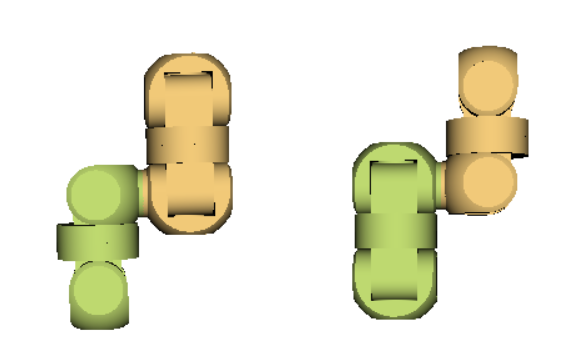
Using this symmetry of shapes allows us to group a large amount of different configurations together. Even one universal module with all joint parameters set to 0 has 16 different valid configurations (without taking different module IDs into account). This number grows exponentially with the number of modules: limiting ourselves to 90° rotations, one module can have 45 different configurations, but only 8 shapes. Two modules have hundreds of thousands of valid configurations, but only about 1500 different shapes.
Topology class
The topology class reduces the state space even more severely, by grouping together all configurations which have the same “topology”. In this case, we only care that each module is connected to the right “neighbours” by correct RoFIComs. We do not take rotations (or even other possible joint parameters) into consideration at all.
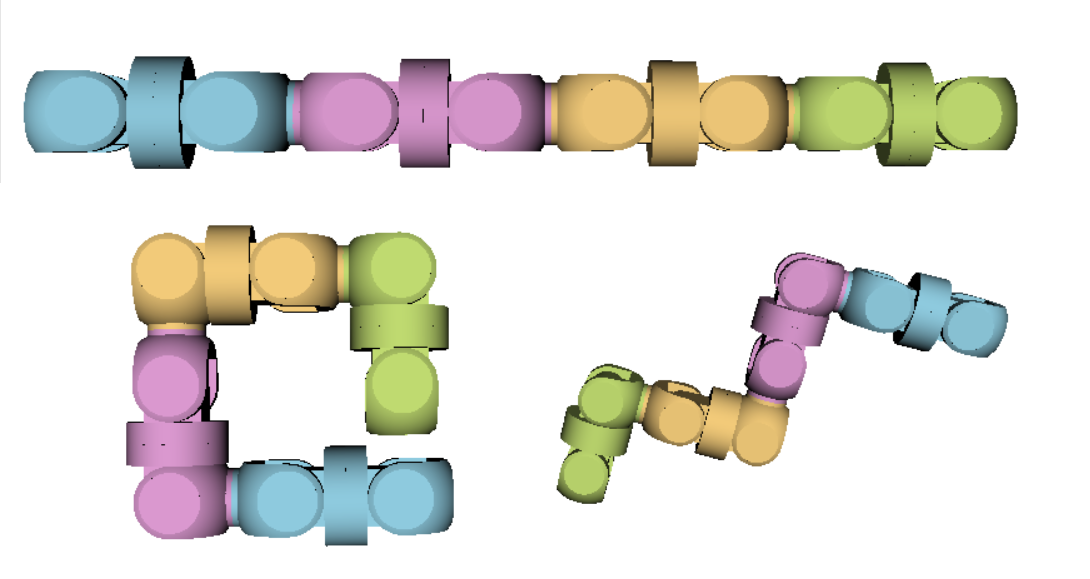
This class also requires us to redefine a step in the state space, as a rotation is no longer a transition between two different equivalence classes. A transition is now made by connecting two previously unconnected RoFIComs, or disconnecting already connected RoFIComs. Therefore we need to be able to reshape the RoFIBot, so it can move a module (or modules) we want to reconnect close enough for the new connection to be made. This can be achieved by using inverse kinematics to generate “reconfiguration subplans”, which include moving a module and reconnecting it, to serve as steps in between different topologies.
